
With the following formula you can calculate how much of the fretboard edge has to be removed when you make the fretboard radius. It's surprisingly little!
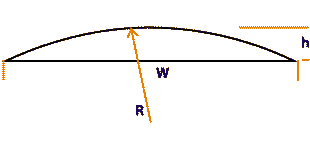
h = R - SQRT ( R2 - 0.25 W2 ) SQRT ... Square root R ...... Fingerboard radius W ...... Fingerboard width
The difference between a cylindrically-shaped and a conically-shaped fingerboard surface is illustrated, or be it slightly exaggerated, in the illustrations below which show the view from the nut towards the end of the fingerboard.

You can see that on the cylindrical fingerboard (1) the fingerboard edge is getting increasingly thinner towards the wider end of the fingerboard. In reality, the difference is less than 1mm, i.e. very small indeed. This also explains why it is possible to file a compound radius into the frets.
If the fingerboard has a compound radius (2), the edges of the fingerboard remain more or less equally thick from the nut to the end of the fingerboard.
With the next formula you can determine the radius that produces the same "h" at the wider fingerboard end as at the nut. Choose for instance a 12" radius at the nut and calculate h with the former formular. Now put h and the width at the fretboard end into the following expression:
h W2
R = --- + ---
2 8h
W ... fingerboard width
h ... calculated "drop off" at the nut
You'll get a radius of approximately 21"
You can for instance calculate the necessary radius for different
points on the fingerboard and make several templates.
Download an universal template for a 12" compound fingerboard radius (PDF-File) wich you can print out, stick on cardboard and cut out afterwards.